Journal Club – Tree Shap

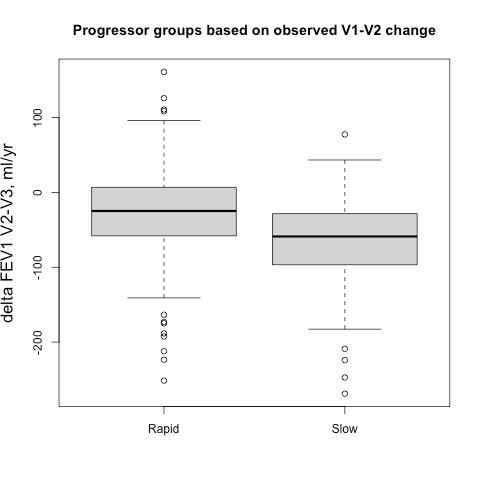
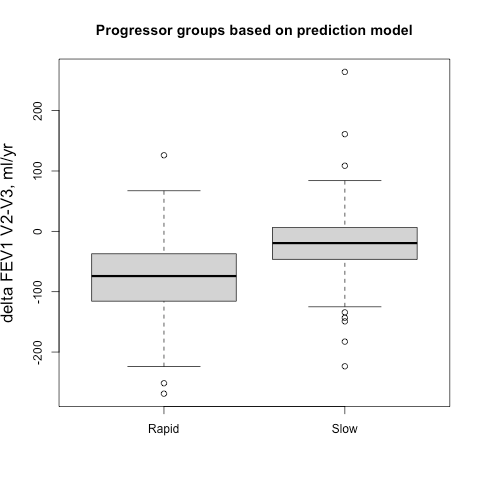
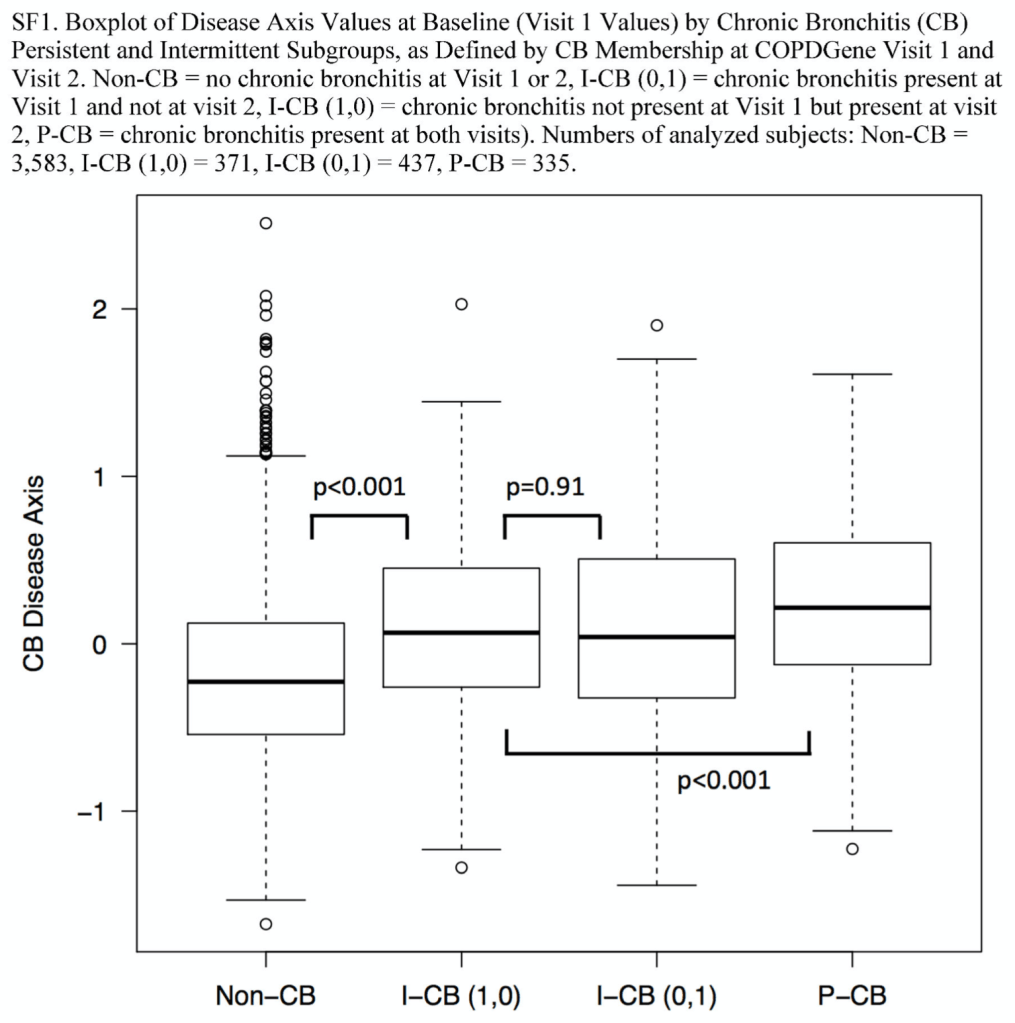
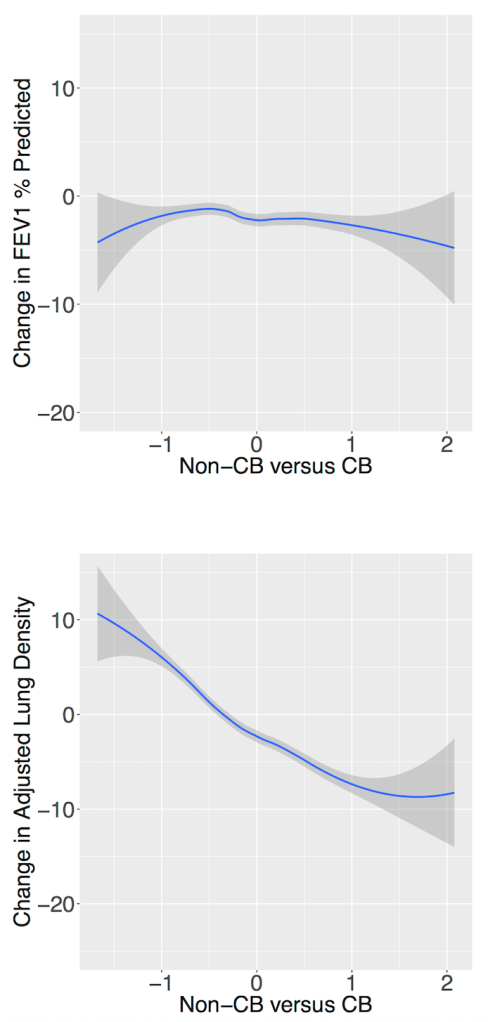
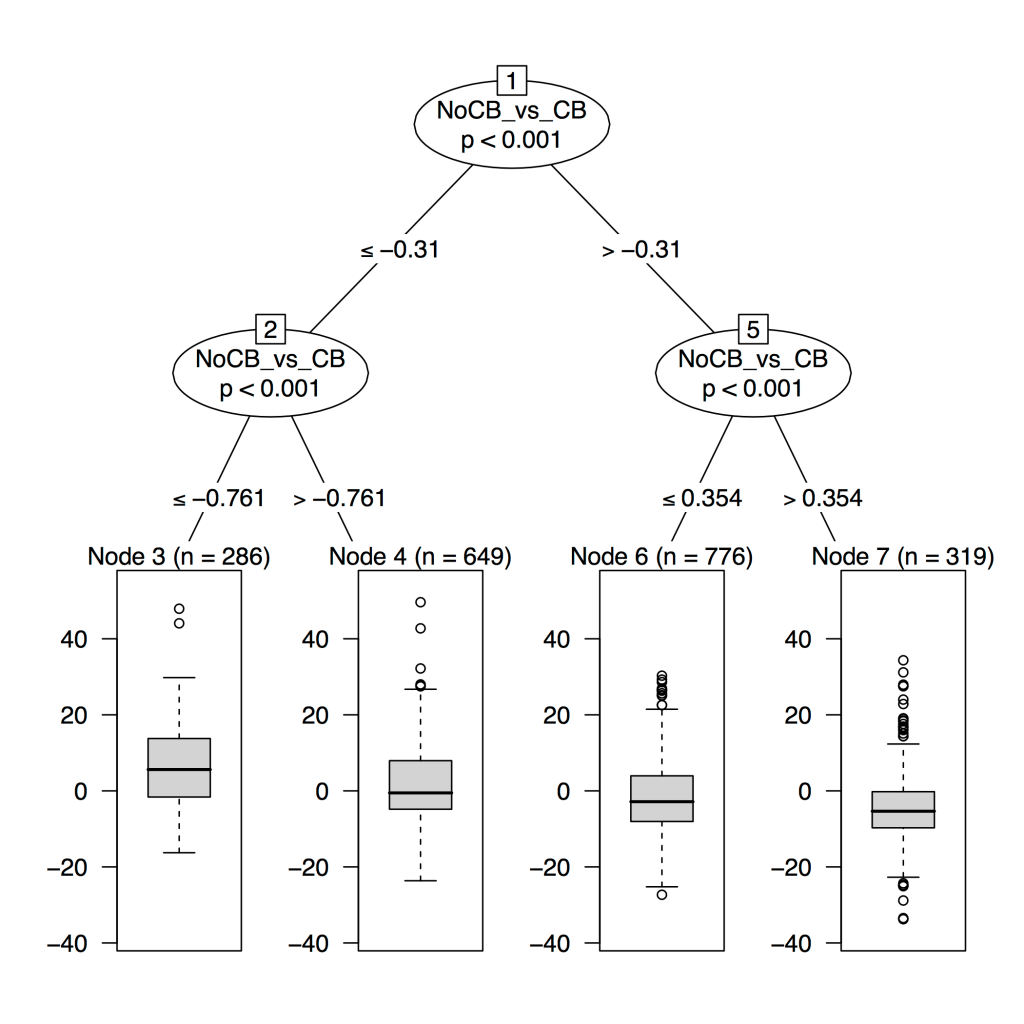
Tree-based models (random forests, XGBoost) are usually among the top performing methods for tabular datasets, so there is substantial interest in this method that claims to compute fast, exact SHAP scores for tree-based models. In reviewing this within our group we spent a lot of time figuring out some specific aspects of proper calculation and interpretion of SHAP scores which will be recorded here for future reference. As shorthand, this method for calculating SHAP scores will be referred to now as the tree explainer.

This post is based on the following papers/sources:

  • The Lundberg 2017 original SHAP paper (“A Unified Approach to Interpreting Model Predictions”)
  • The Janzing 2020 AISTATS paper pointing out a conceptual issue with the original SHAP paper (“Feature relevance quantification in explainable AI: A causal problem”)
  • The Lundberg 2020 paper describing the Tree SHAP method (“From local explanations to global understanding with explainable AI for trees”)
  • The Tree SHAP implementation docs

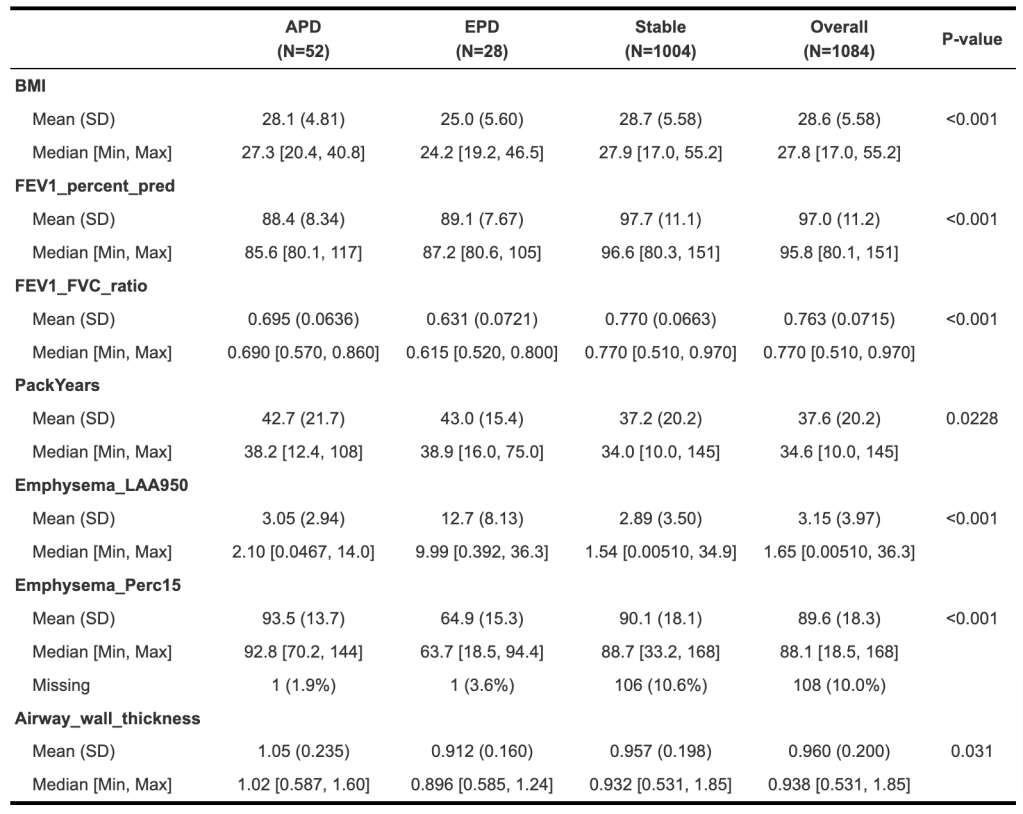
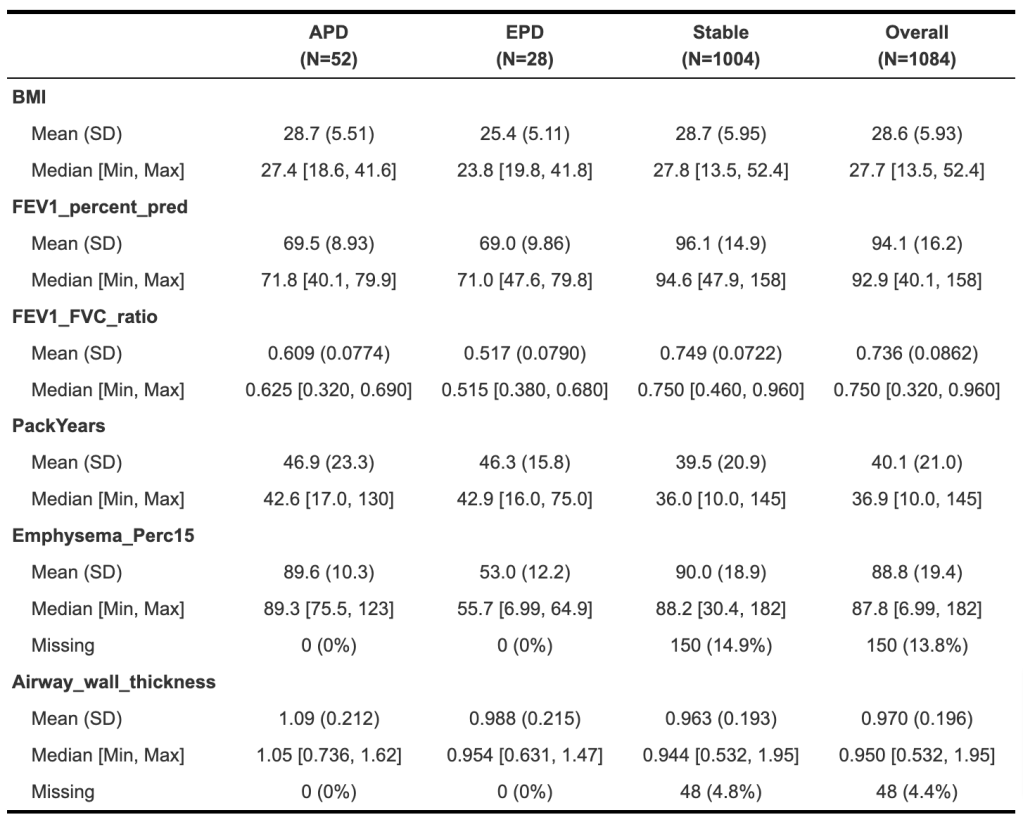
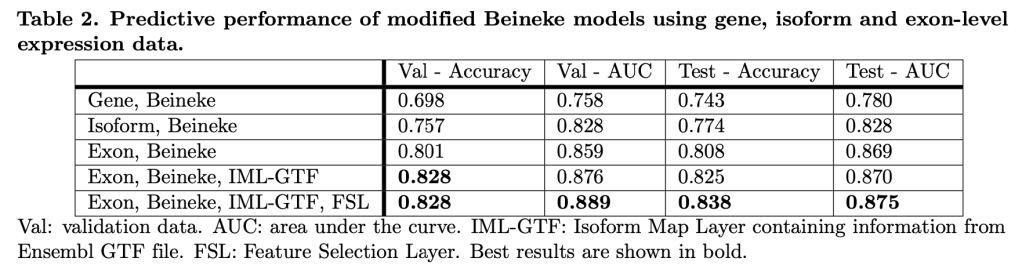
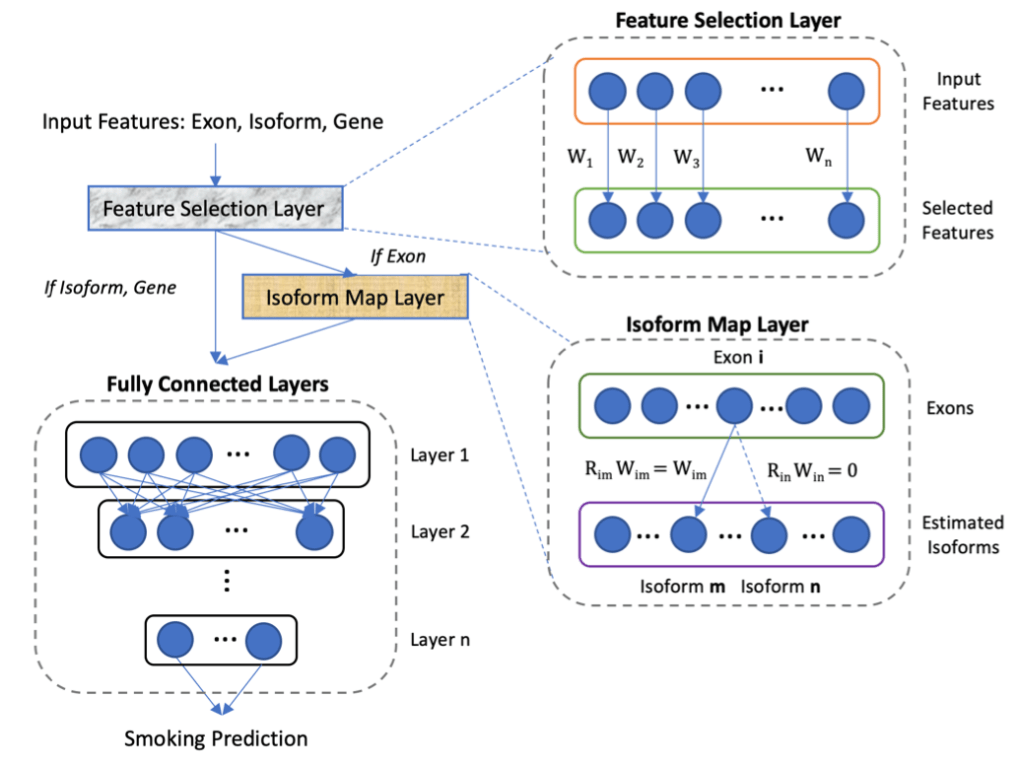
First, how does the tree explainer actually work? First, there are multiple implementations of the explainer, but I think that the “path dependent” implementation is the easiest to understand. This is the algorithm description from a preprint of the paper.

To understand what v,a,b,t,r, and d are, this part helps.

Some important points to make about this:

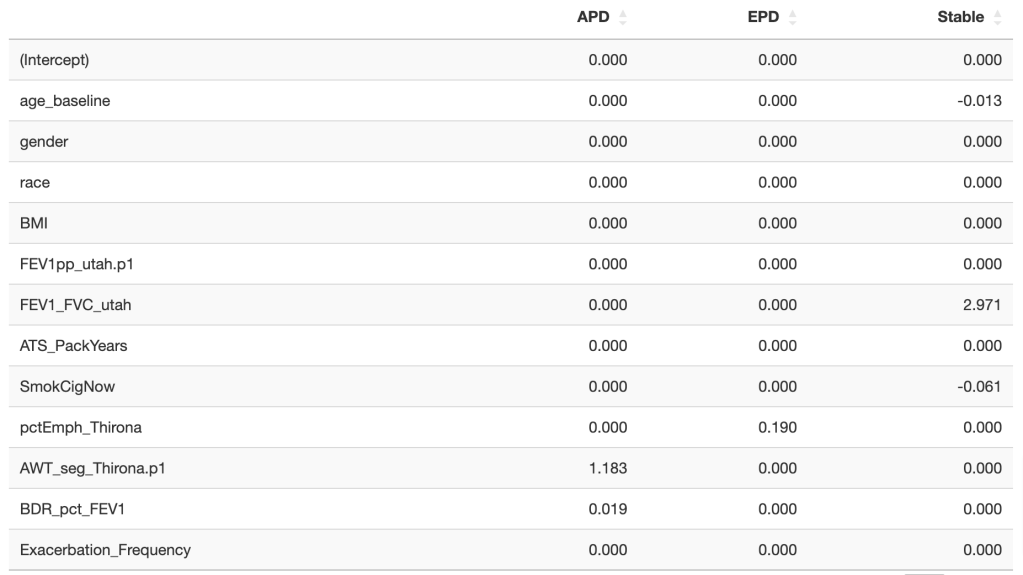
  • This does not require any data, and can be computed directly from the trees
  • It does however require the coverage of each node in order to compute a weighted average. In many tree-based models, this is stored along with the trees and correspond to how many training examples “went through” a given node.
  • “Conditioning on” must be understood properly, and there is a later section dedicated to this
  • Line 9 means that when a feature is being conditioned on, which is the same as being dropped or excluded (if you don’t understand this aspect of calculating SHAP scores, you basically just need to go back to the basics of what SHAPs are and how they are calculated), the way this is implemented in the trees means that “dropping a feature” in effect means replacing that feature with its average, which more specifically translates to the average of its effects in the training dataset.
  • This will then give us a vector of model predictions where the feature of interest is dropped. The vector is of length equal to the number of observations of the feature, and the the SHAP value for each observation will be the difference between the prediction from the full model and the value output by this algorithm for that observation. The resulting vector consists of what we often call “local SHAPs” (observation-specific importance of a feature) and the sum of this vector is the “global SHAP.” (total importance of a feature over all observations of interest)

If you’re following along with the original paper, we skip discussion of the next algorithm (Algorithm 2 in the paper), which the authors claim to simply be a more computationally efficient (but empirically equivalent) implementation of the algorithm we just reviewed.

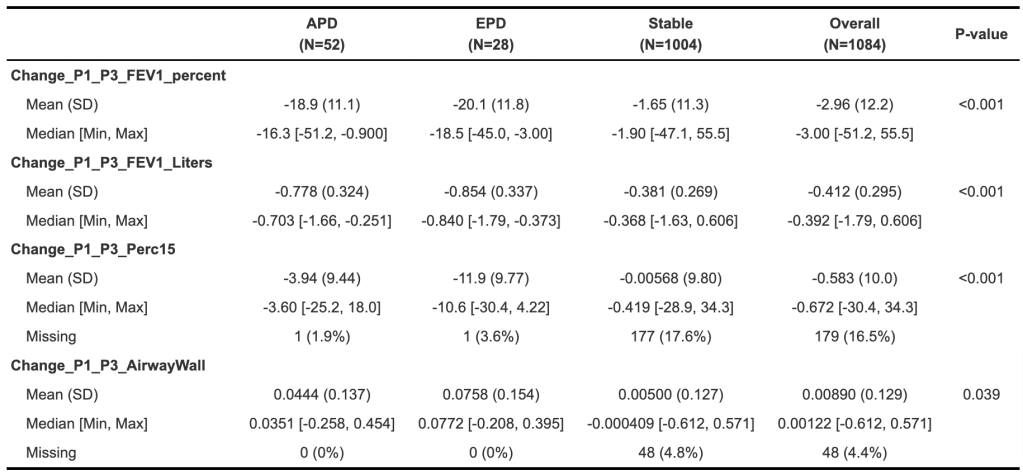
Things get interesting (in a scientific method, gossipy kind of way) with Algorithm 3 (Tree SHAP with interventional perturbation). For reasons I don’t fully understand (TBH), the interventional perturbation algorithm is necessary if one wants to calculate SHAP values not for the model’s direct output, but for a nonlinear transformation of the model’s output. It seems like Algorithm 3 does what Algorithm 2 does, but it does this by iteratively looping over individual observations (which means real data, not just the trees, is required). This is described here.

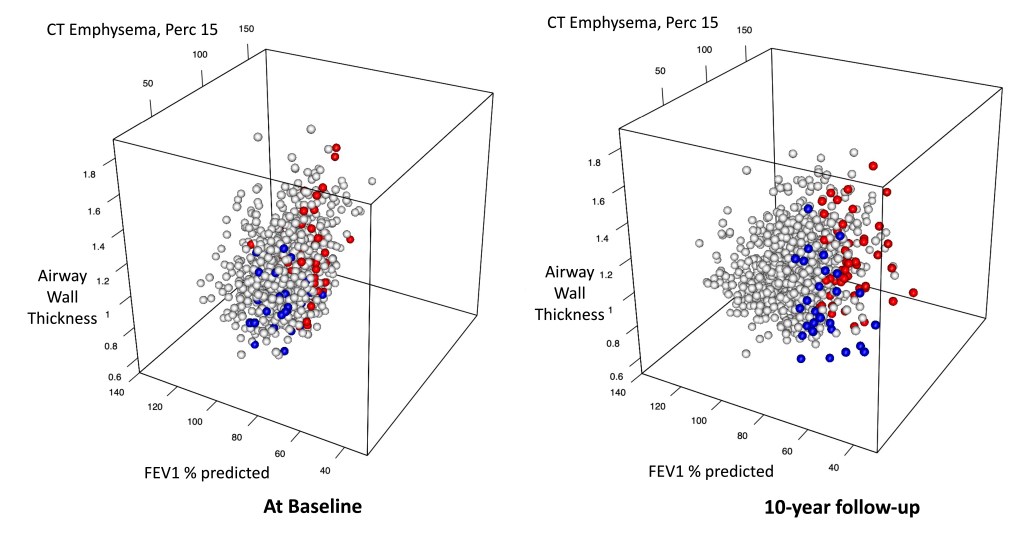
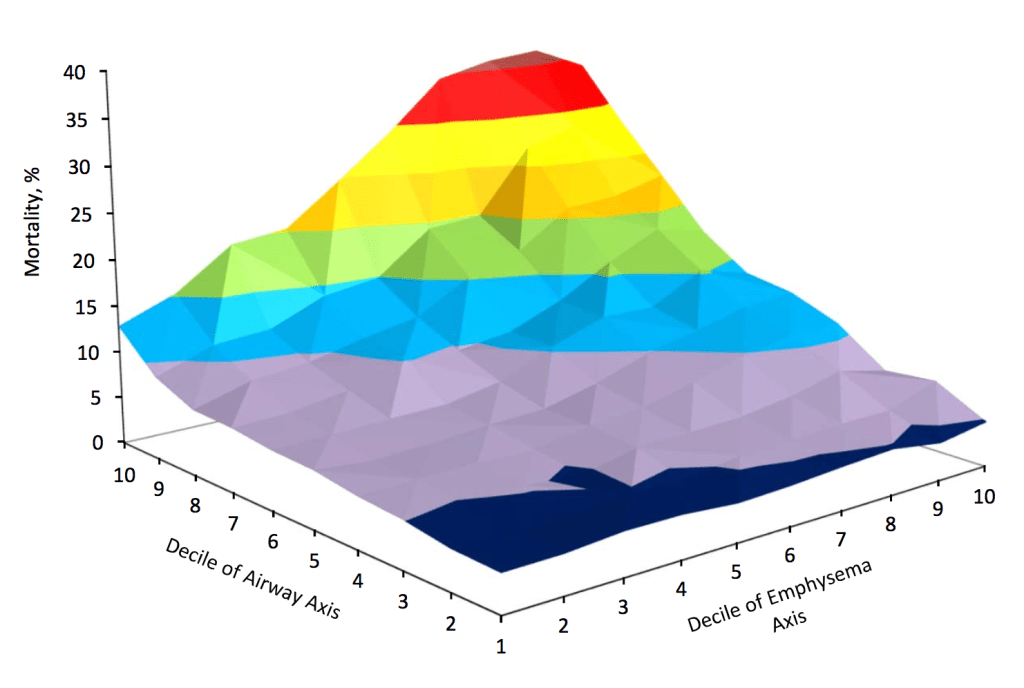
The gossipy interesting part is this. In the original SHAP publication, the authors theorized that the best way to compute SHAPs would require having access to the conditional expectation of the model prediction. What is this? It is the average prediction that the model would make if the variable of interest (the one being conditioned on) was not available to the model. One way of thinking about this which is not exactly correct I think is that, in order to calculate this, we need to know what the prediction of the model would be for each observation if one feature was removed and the rest of the feature values were the same as they actually were for that observation. Since it is hard to compute the conditional expectation, the authors in the original paper basically did the right thing for the wrong reason – namely the used the marginal expectation instead claiming that would be OK if one assumed that all features were independent. In this subsequent paper, a different set of authors explains that the marginal expectation was actually the right thing to use all along, and that people had been and were still at risk of making future errors by trying to “improve” SHAP methods by using the conditional expectation. The relevant portions are included below.

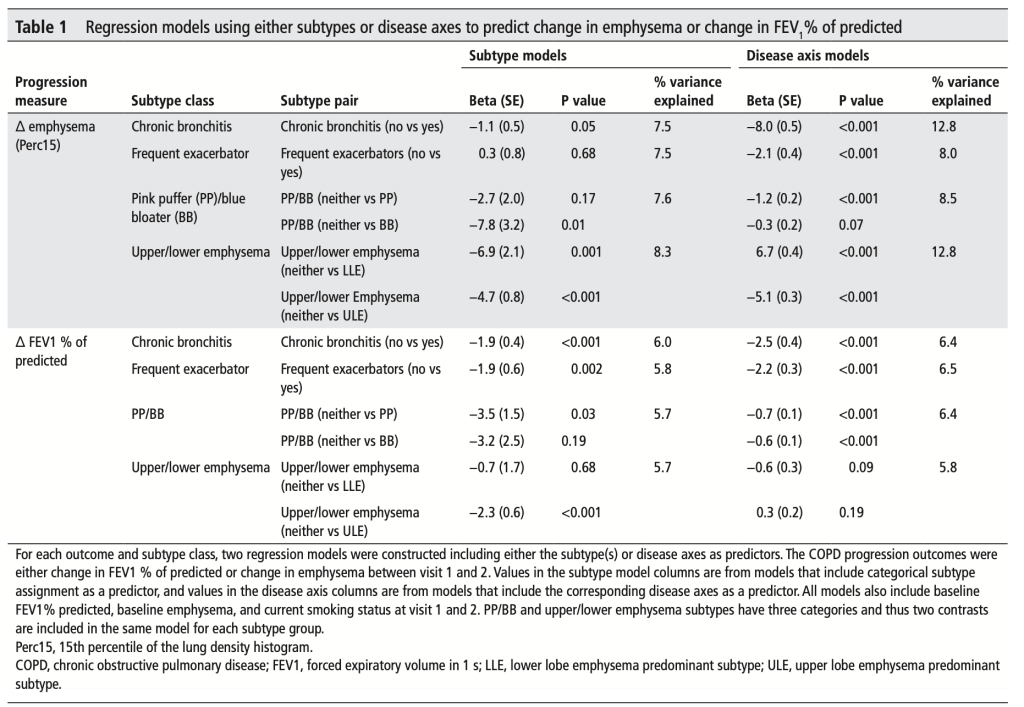
The key thing here is the reference to causal theory and the do-operator. The practical point is that by using the do-operator, we can calculate the expected prediction for a specific value of a variable (a specific value of x1 for a variable X1 that we wish to get a SHAP value for), accounting for the full joint probability distribution of x2 and x3 (or the rest of the features, however many there are). I think the reason why this is called an interventional conditional distribution is that do-operator allows for us to intervene on X1 by enforcing a specific value in a manner that is robust to spurious attributions of importance that can arise from correlation patterns in observational data that can arise from unobserved variables. Some important points that follow from this:

  • In the shap.TreeExplainer implementation, when feature_perturbation is set to “interventional”, this is what is being done and the reason why real data are needed is in order to get a reasonably accurate estimate of p(x2,x3), i.e. the multivariate distribution of all of the variables (except for X1).

Some other open questions.

  • So what data should we provide when we are using the tree explainer?
    • Some relevant info: It seems that the “expected_value” used in the tree explainer comes from the model itself, not from any specific provided data. This depends on the model object including the coverage for each node, and this means that the expected_value is equivalent to the mean of the predicted values in the training dataset (accounting for in some methods some random variation from random sampling in the training procedure, as discussed here).
    • Assuming the thing above, then the main concern for what sort of data to provide relates to the “interventional” behavior described above, which means that it is probably not every really necessary to provide the entire training dataset to the tree explainer.
  • end

petecastaldiLeave a comment

Splicing postdoctoral fellow job description

Principal investigators: Peter J. Castaldi, MD, MSc; Yohannes Tesfaigzi PhD

Job Description

The Castaldi lab within the Channing Division of Network Medicine (CDNM) and Brigham and Women’s Hospital is seeking to hire a postdoctoral associate to take a leading role in an NIH R01-funded research project focused on the identification and functional characterization of genetic variants that alter risk of Chronic Obstructive Pulmonary Disease (COPD) through effects on splicing. The project is a multidisciplinary collaboration in which genome-scale analysis led by Dr. Castaldi is coupled with basic science investigations in airway epithelial cells led by Dr. Castaldi’s long-term collaborator, Dr. Yohannes Tesfaigzi. The candidate will have the opportunity to define their own research program within the context of multiple NIH-funded research projects focused on the functional characterization of COPD GWAS-associated variants in airway epitheial cells. This project will involve working with existing and newly generated long read RNA-sequencing datasets and single cell RNA-seq data from both large-scale human cohort data (COPDGene and the Lung Tissue Research Consortium) and the largest available collection of primary human airway epithelial cells from 190 human subjects. The associate will work closely with Dr. Peter Castaldi, an established continuously NIH-funded investigator with an excellent track record in mentorship for both academic and industry placements, in a rich research environment at BWH and Harvard Medical School with a network of close collaborators (including Dr. Yohannes Tesfaigzi and Dr. Aabida Saferali) with expertise in respiratory epithelial biology, long read sequencing, proteomics, and computer science.

Requirements

• PhD in Biology, Statistical Genetics, or Computer Science

• experience with the analysis of genomic data, including genetic association and QTL studies

• knowledge of RNA splicing, long read sequencing, and/or proteomics is a plus

Candidates should contact Peter Castaldi at: channingpostdoc.pjc@channing.harvard.edu

All qualified applicants will receive consideration for employment without regard to race, color, religion, sex, sexual orientation, gender identity, national origin, disability or protected veteran status.

petecastaldiLeave a comment

How well can we predict the development of COPD subtypes?

COPD usually progresses slowly over decades, and we really don’t know much about how COPD progresses with respect to important aspects of the disease such as emphysema and airways involvement. Most of what we currently know about the epidemiology of COPD development comes from large population-based studies with longitudinal spirometry (studies like the Normative Aging Study, the Framingham Heart Study, the Lung Health Study, Copenhagen City Heart Study, and others). These studies show a smooth decline in lung function starting at around age 30, with notable variability in both the rate of decline and in the level of maximal lung function achieved. Both factors (rate of lung function loss and maximal lung function attained) are now recognized to be important in accounting for the development of COPD. However, because there has been essentially no information on longitudinal changes in lung CT scans, we know very little about how different types of COPD develop. The purpose of this brief report is to review some data from COPDGene describing the progression of smokers without COPD into two distinct types of COPD, emphysema and airway-predominant COPD.

COPDGene is the largest COPD-focused study to have longitudinal measurements of chest CT and spirometry, so here we analyze data for 1,084 subjects in GOLD Stage 0 or 1 at baseline. We’ll use data from the baseline and 10-year visit to answer the following questions:

  • How many subjects developed COPD over this 10-year period?
  • How many developed airway-predominant COPD (APD) and emphysema-predominant COPD (EPD)?
  • How well could these subjects be identified at baseline? Can we predict the development of COPD and APD/EPD over a 10-year period?

Some definitions: Airway-predominant COPD = GOLD stage 2,3, or 4 + CT Emphysema <5% (by LAA-950).

  • Airway-predominant COPD (APD) = GOLD stage 2,3, or 4 + CT Emphysema <=5% (by LAA-950).
  • Emphysema-predominant COPD (EPD) = GOLD stage 2,3, or 4 + CT Emphysema >=10% (by LAA-950).

The folks in between we refer to as Mixed COPD. This was the least common group and isn’t included in this analysis. The link to the paper establishing these definitions is here. One additional complication is that the COPDGene 10-year visit CT scans were obtained at a lower dose than previous visits due to changes in imaging standards. As a result, LAA-950 measures are not available at the 10-year visit and we had to modify the definition to use Perc15 CT Emphysema cutoff values that were selected to approximate the 5% and 10% LAA-950 thresholds.

We also need to describe the characteristics of the subjects at baseline, including some basic details about disease progression as well. The significantly different characteristics between groups are shown below.

Keeping in mind that these subjects were selected to be in GOLD spirometric stage 0 or 1 at baseline, we can see that the subjects destined to progress to APD or EPD have lower FEV1 % predicted values and greater pack-years exposure. Specifically for EPD, these subjects have markedly more emphysema and lower BMI. APD subjects do have thicker airways, and the EPD subjects have smaller airways than the “Stable” group that will not progress.

Now let’s take a look at how these subjects look 10 years later.

Finally, let’s look specifically at measures of 10-year change.

We should remember that some of these changes are built into the subject selection – we are specifically focusing on subjects that started in GOLD 0 or 1 and progressed to GOLD >=2 COPD of the APD or EPD subtype. So the fact of certain changes such as loss of lung function is less interesting than how things have changed. The most notable thing here is that the APD subjects have lost FEV1 without gaining much emphysema or airway wall thickness (these are segmental airways, FYI). The other notable thing is that the EPD group has developed more emphysema, and more interesting their airway walls have thickened the most. Take home lessons:

  • Emphysema begets emphysema.
  • As subjects enter into COPD, emphysema begets airway wall thickness (big caveat is this is segmental airways).
  • The airway-predominant subjects lose lung function without gaining emphysema or having obvious increased thickening of the larger airways. We don’t know what’s driving this progression.

In the image below we see these subjects projected into the 3D space defined by FEV1 % predicted, emphysema, and airway wall thickness. Subjects who progress to EPD are blue, APD is red, and stable subjects remaining in GOLD 0/1 are white.

The 10-year progression to APD/EPD is 80 subjects out of 1084, that’s 7% of the study sample. As a reminder, the other progression group to COPD is the Mixed group (emphysema between 5-10%), though this group was smaller than either APD or EPD (n=14 subjects). If we extrapolate those numbers to the population of heavy smokers over 50, this translates to a lot of people at the population level. At the moment, these data are one our best current approximations of how the APD and EPD subtypes develop in the population of older smokers. For the development of preventive treatments, the billion dollar question is whether we could actually identify these subjects prior to disease progression when they could be treated early in disease when they have lots of nice lung left to save.

To address the question of early identification we used the elastic net approach to construct models to predict APD, EPD, or Stable status at 10 years using baseline predictor data. Since we only have 28 EPD and 52 APD instances, we weighted each point by the inverse of its frequency in the dataset (for example for EPD each point receives the weight: 1/(28/1084)) and we used five fold cross validation in the model building process. We only considered 12 predictors, but still these results are at risk of overfitting and will require validation or ideally re-estimation when more data on 10-year progression to APD/EPD become available. The final coefficients of the models for each subtype are shown below (FEV1pp_utah = FEV1 % predicted, FEV1_FVC_utah = FEV1/FVC, SmokgCigNow = current smoking status at baseline, pctEmph_Thirona = LAA-950, AWT_seg_Thirona = segmental airway wall thickness, BDR_pct_FEV1 = bronchodilator response).

Using standard clinical variable plus CT measures of emphysema and segmental airway wall thickness, model performance in cross-validation was decent but not great. Given the class imbalance we’ll report the AUPR curve values (area under the precision-recall curve), which were 0.09, 0.34, and 0.86 for APD, EPD, and Stable subjects, respectively (one versus all). A more intuitive representation is to report the percentage of incorrect classifications that would be required to recover 50% of each class. These numbers are 92% and 78% for APD and EPD, respectively. It helps to recognize that in this study the baseline prevalence of the “destined for APD” and “destined for EPD” GOLD 0/1 subjects was 5% and 3%, respectively. So we’re talking about roughly 2-fold and 7-fold enrichment from these models, but the reality is that one would need substantially more effective enrichment in order to have a clinical trial where say 50% of the enrolled subjects would progress to the desired subtype (over 10 years).

petecastaldiLeave a comment

Crossover designs, saxophones, resonators, and musician perceptions

Journal Club: Plastic or Metal? Saxophone pad resonators

Brief summary: Fun discussion about study design and randomization as it relates to crossover study designs. The article is a study of musician perceptions on a kind of modification to saxophones called “resonators.” This study was introduced to me by my friend Allan Walkey, a pulmonologist, health services researcher, and a pretty good sax player as well. Thanks to Gary Scavone, the senior author of the study who joined us at the end to give his insights!

Guests: Allan Walkey (AW) – https://www.bumc.bu.edu/pulmonary/about-us/people/allanwalkey/

Gary Scavone (GS) – https://www.mcgill.ca/music/gary-scavone

Article Links:

http://www.music.mcgill.ca/caml/lib/exe/fetch.php?media=publications:eveno_pads_aaa_2015.pdf

Plastic or Metal? Pad resonators blind test | Inside the saxophone

PC: I loved this study, which was presented in two separate posts online and as a full paper. I thought it would be fun to start journal club with something non-medical. I’ll explain my positive response to it. The two things I liked most about this study were:

  1. The question is incredibly clear and the practical importance is obvious. Do I need pad resonators for my saxophone and if so, what kind?
  2. The elegance of studying the question on multiple levels.

To expand on the second point, there is “objective” data (measurements of impedance, amplitude, and efficiency) and there is “subjective” data on musicians assessment of “brightness.” To translate it into the biomedical realm, it was like a paper where a convincing trial outcome is also supported by a strong and plausible biological mechanism. What was your main reaction?

AW: OK, first a little (OK, a lot of) background. What are resonators? When each key on a saxophone opens and closes, it changes the note. A closed key uses a leather pad on the bottom to make a seal so no air escapes and the note is strong, in tune, and doesn’t squeak. If you imagine a sax with closed keys as a metal tube that conducts sound, you can also imagine that the material on the bottom of the closed keys might matter in terms of the quality of the sound being produced. Additionally, you might expect a ‘dose response’ in which the more keys that are needed to produce a note the greater the effect on the quality of the sound. “Resonators” are material placed over the center of the leather pads on the bottom of the keys and are designed to reflect the sound from the closed key back through the horn. More accurately, they are ‘sound reflectors’ than resonators. You can buy resonators in brass, nickel, silver, gold, plastic, or use no resonator and go with all leather on the bottom of the key.

About 15 years ago I graduated medical school, started residency, and was excited to buy myself a present for completing my intern year: my first professional-grade alto sax. After some initial research I bought a Yamaha unlacquered ‘custom Z’ sax (saxophones are typically coated in a coat of lacquer to maintain a shiny finish, which can change the sound) in order to try to get the purest most free-blowing sound unencumbered by the vanity of lacquer. So I was a little disappointed when I saw that my new sax arrived with plastic resonators on the pads, rather than ‘pure brass’. My dream of having the purest sax sound in history was foiled by this unnatural plastic underneath my keys! From that moment, I dreamed of the day that I would place metal resonators on my horn to allow it to realize its full brass potential.

Fast forward to today. After 15 years of wear and tear (on me and my sax), my pads were literally torn up, the springs rusty, and my sax was in need of an overhaul. In an overhaul, a sax is disassembled, cleaned, oiled, and the pads and springs are removed and replaced with new fresh parts. It’s a big, expensive  job that takes a sax repair person probably a week of work. But I saw this as an opportunity – while my sax was disassembled, (for about $150 extra) I could have new metal resonators placed to finally achieve my brass dreams. 

Would it be worth the expense and changes from my 15 years of familiarity with my plastic resonator sax to make the change?

PC: Ahh. Now I know what a resonator is! So this was the question that brought you to the article. Two questions – 1) how did you find it? And 2) what did you think of the article?

AW: 1) I just Googled “do sax resonators make a difference” or something like that. And the first hit was this article called “plastic or metal”. It was posted in the website of Syos, a company that makes custom sax mouthpieces, and I thought it was going to be an advertisement for a new line of resonators. But it wasn’t. It was a summary of a “real” research study. 

2) This was a “practice-changing” study for me. It used a mixed-methods approach (similar to what we use in our own research center) of quantitative analysis and qualitative evaluation of stateholder perceptions to get a full “picture” of the effect of different resonator materials on sax sound quality. It used randomization, blinding, and a within subjects crossover design to minimize both random and systematic bias. It had clear figures and presentation of results. Finally, the results seemed unambiguous. In some ways, the “negative” result here reassured me that this study was not biased by commercial interests. 

PC: Some interesting points there. Let’s talk about the study design, and specifically as it relates to the results in this figure.

To fill in some detail, you have four different saxophones with three outcomes. Saxophone 38 is the “control” (no resonators), sax 40 has metal resonators, and for some reason both sax 37 and 39 have plastic resonators. Each saxophone is then graded according to three measures by 13 musicians. It’s interesting to think how this could be translated into a typical randomized clinical trial. The way I see this, the saxophones are like people, and the resonator status is like the treatment or exposure. The ratings from each of the 13 musicians are the study outcomes. So, if you look at it this way, it’s not quite as good a study as it could have been, because the randomization is done only with respect to the outcome measurement, but not respect to the saxophone and the “treatment.” Do you agree, or do you see it differently?

AW: Interesting. I saw it differently. To me the musicians were the subjects (their perceptions are being measured), the 4 different saxes were the treatments or exposures (plastic, metal, or none), and the outcomes were the 3 different perceptions: brightness, evenness, and ease of play. So I viewed this as a 13 subject, randomized, blinded, crossover study in which the treatments were identical saxes with different resonator types. For these perception outcomes, the scale is 0-1, and the best sax had to get a 1 and worst a 0. They repeated the measurements for each player. In the full manuscript there are lots of additional results, including intra and interindividual concordance ratings for each criteria, results according to sax experience, as well as repeated measures anova for main results. There’s some interesting results hidden there as well. 

PC: Got it. My point is that technically they are not “identical” saxes. In this study, the specific saxophone and the exposure (resonator type) are perfectly confounded. But I think you are saying that, if one assumes that the saxes are identical, then this isn’t a problem. But if that’s not a safe assumption, then I say this is a potential problem, and if it would be easy to swap out resonators (is it?), it would have been better to randomly assign the resonator to different sax/musician pairings. So, if one were to distill this down to a single concept, it is that the purpose of randomization is to address confounding that cannot be handled in other ways, but that proper randomization must be done with respect to your exposure. In other words, the randomization must intervene between your exposure and your study subjects, which is why it is important to decide whether we think the study subjects are the saxophones or the musicians here. Capiche? I drew up my conception of three ways of viewing the study (shown below). The first one is my idea of your view, the second and the third are alternate ways of assigning labels of study subject and treatment/exposure. The interesting thing about the third one is that, in this study, the people are essentially viewed as the equivalent of laboratory equipment – they are the measurement device that gauges the effect of the different resonator types. My contention is that the most accurate way to represent the study is option 3, but that in reality none of these is the optimal study design (which I would be happy to expound on). But I would say that if one is willing to assume that the saxophones are truly exchangeable, then I think options 1 and 2 are both defensible. The problem with 3 is that the intervention is not located in its proper place between study subjects and the exposure of interest. Thoughts?

AW: Right, an individual sax = resonator type. So there is potential confounding by sax. In the investigator’s defense, they use the same exact model, with consecutive serial numbers, and then test them for acoustic qualities at baseline and there seems to be no objective difference in sound before they switch out the resonators. But there’s still a risk of confounding by intrinsic sonic differences to each sax. It’s not easy to switch resonators. One way to reduce the risk of confounding by sax further would be to have 2 saxes for each resonator exposure because it would be unlikely that random variation in sax sound would correlate between 2 saxes. They do this only for plastic resonator, but results are reassuring since they are similar for the 2 plastic resonator saxes. I’m having a little trouble with your figure. It seems strange to me to say the study subjects are the resonators. It’s like saying the study subjects are the drugs under study. Yes, resonator is the study subject, but the subjects that are subjected to the treatment (resonator) here are the musicians. The sax here is just a delivery device for the treatment (resonator). 

Let’s make an analogy: You want to know if inhaled albuterol (plastic resonsator), inhaled ipratropium (metal), or inhaled saline (no resonator) result in different perceptions of breathlessness for people with asthma (musician). In a random order (to account for confounding by order effects), you have 13 asthmatics use the albuterol inhaler, the ipratropium inhaler, saline inhaler, and another albuterol inhaler and they rate breathlessness on a scale. Now you could say – wait! How do we know that the inhalers themselves don’t work very differently to deliver the medication! Which is a good point, but  we can be reassured by prior testing of the inhaler and that the same factory made them all, etc.   

So our causal diagram to me, is as follows:

If we assume that confounding by musician differences is taken away by the within-subject design (i.e., exposure of all musicians to all resonators and saxes), that differences between saxes is negligible (like differences between the same model inhaler), and order effects are taken away by randomized order, then there should be negligible confounding to this study.

Thoughts?

PC: I like it. I actually completely agree after hearing you explain it that way. I think the key for helping me understand it is to key in on the musician as the subject (natural), which then highlights the crossover nature of the trial (everybody experiences every resonator), and also highlights that the randomization is related to the order in which they experience the resonators to account for that potential bias, as your diagram illustrates. So to return to the original diagram, #1 is the right way to think of the study, and saxophone is theoretically a perfect confounder, but if one is willing to assume it isn’t then it is a good study! One could also imagine a way in which the relationship between sax and resonator could be randomized so as to avoid that bias, but perhaps that is not a matter of practical importance. On that note, let’s hear some thoughts from Gary Scavone, the senior author of this study.

GS: I helped organize and supervise this study, so I can add a few perspectives on the design: 

The saxophones were loaned for free by Yamaha for the study. As mentioned in the paper, they were consecutive serial numbers off the manufacturing line of a well respected company and their tolerances seem to be quite low, so they are about as similar to one another as could be expected. That said, when I was looking to buy a new Selmer saxophone back in 1989, I tried 6 different horns in a shop in Bordeaux and finally settled on one that “seemed” the best match for my priorities. It is hard to compare horns quickly, as you have to set one instrument down, take the mouthpiece off, put it on the next instrument, and so on. I remember thinking that there were some slight differences between those saxophones but nothing super significant. For sure, metal saxophones made on manufacturing lines are significantly more similar to each other compared to instruments made from wood and by hand (such as violins), due to natural variations in the materials. When we received the 4 Yamaha saxophones, I tried them all and could not detect any particular differences between them. My feeling was that either Yamaha has better tolerances than Selmer and/or the manufacturing process has become more consistent compared to the 1980s.

More importantly, in my opinion, is that all 4 saxophones came with plastic resonators. Thus, we had to send 2 of them to a shop to have the pads changed. That was the biggest weakness of the study because we cannot say for sure that extra variations between the horns were not introduced during that process. We even had an issue with leaks after the new pads were installed and had to take one of the horns to another shop to get it adjusted. I don’t know how this limitation could be minimized, but it was an issue.

That all said, when I played the 4 saxophones myself, the horn without resonators was very noticeably “darker” in tone quality, while the other 3 were relatively similar to each other. I was not one of the subjects in the study but I was not surprised by the results … this was one of the clearest perceptual studies with musical instruments that I have supervised. We have done many other studies with violins and it has normally been hard to get consensus on the results due to large variations in preferences.

PC: Thanks Gary. One of the things that strikes me is that, as much as we try to put all of the relevant information into our scientific papers, I rarely speak to the authors of a study directly without getting some useful insight into matters of practical importance. It’s interesting to hear your point that, on the scale of things that you have studied in this way, the effect of the resonators was large and pretty clear. With respect to saxophone as a potential confounder, it sounds to me like it’s possible but not particularly likely based on your and Allan’s previous experiences and perceptions of variation between saxophones. During the course of our discussion we touched on issues related to the design and analysis of crossover studies, and I’d like to return to this in a future post if we can get some of my statistician friends to join, but I think this is a good place to end our current discussion. Again, really appreciate your time and input here Gary, and congratulations on the work you and your group did on this very interesting and well done study.

So Allan, let’s end with the real world implications of this work on an end user. This all started with your question, “Would it be worth the expense and changes from my 15 years of familiarity with my plastic resonator sax to make the change?” So what did you end up doing based on reading this study?

AW: I discussed putting on metal resonators with my sax repair guy. His opinion was also that the material of the resonator did not seem to be very important, but thought size might matter (for resonators). He sent me links to many different choices in different textures and finishes. Depending on the type of resonator, a switch to metal would add between $75-150 to the cost of the overhaul. Because I was unsure if or how new resonators would change my sound, I elected to stick with my old plastic ones. 

PC: And there it is. Science in action. Enjoy your overhauled sax Allan!

petecastaldiLeave a comment

Predicting COPD Progression: Impact of regression to the mean for noisy variables

One of the holy grails of COPD research is being able to identify “rapid progressors”, i.e. individuals who are destined for rapid loss of lung function. One of the challenges in doing this in COPD is that the rate of disease progression is usually slow, so that it (probably) takes years of observation to distinguish a “rapid progressor” from a “nonprogressor.”

In the COPDGene Study, our spirometric datapoints come at 5-year follow-up intervals. After the COPDGene 5-year study visit, there was great interest in being able to identify “rapid progressors” who could be studied intensively at the 10-year visit. At first glance, it might seem natural to look for rapid progressors in the set of individuals who had the greatest lung function decline between visit 1 and visit 2; however as I show below this approach can backfire pretty badly, and it’s a nice illustration of both regression to the mean and the practical importance of measurement error. The three COPDGene study visits are shown below. When we built the prediction model we were at the 5-year time point using the visit 1 and 2 data to try and predict behavior at visit 3. Now, we have roughly have of the visit 3 data available to us, so we can learn some things about how successful we were at prognosticating from the five-year visit.

When we tried out different ways to identify rapid progressors, we compared two approaches: 1) Defining rapid progressors based on the observed change in FEV1 from Visit 1 to Visit 2 (observed delta FEV1V1-V2) or 2) Defining rapid progressors based on the predicted change in FEV1 (predicted delta FEV1V1-V2) using the output of a random forests model using a standard set of clinical and radiographic predictors. The model’s fit to the observed delta FEV1V1-V2 was pretty good. The scatterplot is shown below, and the model explained 87% of the variance of the observed delta FEV1V1-V2.

The real question though is how well the model predicted future change in lung function, i.e. the FEV1 change from V2-V3 (observed delta FEV1V2-V3). Here is the correlation of the observed delta FEV1V2-V3 to predicted delta FEV1V2-V3 obtained by using V2 values of the predictor variables entered into the same prediction model as described above. This model explains 10% of the variance of observed delta FEV1V2-V3.

Not great. But interestingly so much better than using the observed delta FEV1V1-V2 to predict the observed delta FEV1V2-V3. Take a look at the correlation between those two below. It’s negative! In other words, if you want to find rapid V2-V3 progressors, you’d be better off selecting SLOW V1-V2 progressors than you would be selecting rapid V1-V2 progressors.

Sometimes it easier to see this when subjects are broken into groups, so we identified groups of 500 fast and slow progressors (stratified by gender to account for differences in lung size) according the their observed delta FEV1V1-V2 and their predicted delta FEV1V1-V2, and then we compared the prospective 5-year progression of these groups (observed delta FEV1V2-V3). These results are shown side-by-side below. It’s apparent that for the groups defined by observed change you actually get the opposite of what you want. The slow group progresses more rapidly over the next five years, but if you rely on the output from the prediction model you get the desired behavior. A t-test comparing the V2-V3 FEV1 change between rapid and slow groups is highly significant.

This is simple regression to the mean, but can still be counterintuitive. We had to look at the data a bit to really absorb the magnitude of this effect. I think one of the learning points here is that when FEV1 is observed only twice over relatively short time period, the delta FEV1 variable can be really noisy. When cutoffs are applied to a variable with low signal to noise ratio, the selected subjects at the extremes of the distribution also happen to be the ones with the largest measurement errors. Those subjects are not actually the ones with the greatest rate of “true progression,” they are just the ones with the largest measurement error that, by virtue of the thresholding, tend to all be aligned in the same direction. Then, if the measurement errors at visit 2 and visit 3 are independent, then the measured FEV1s of those subjects will move in the opposite direction at the next time point since those measurement errors will be evenly distributed around a mean of zero.

petecastaldiLeave a comment

Interpretablity in machine learning for genomics

“All science is either physics or stamp collecting.” The implication of this famous quote, attributed to Ernest Rutherford, is that physics, with its mathematical quantification of natural laws, is superior to disciplines like biology that accumulate observations without synthesizing them through mathematical description. From this math-centric perspective, the data revolution in biology is a step up the purity ladder towards physics and away from the social sciences. Despite the odiousness of this reductive view, the biology-physics analogy is enlightening to the extent that it prompts critical thinking about where biology is headed and what the phrase “biology is a data science” might imply. Can the proliferation of new biological data be leveraged to discover the fundamental rules that govern biological systems? Or will we simply end up with billions of stamps and expensive storage bills?

https://imgs.xkcd.com/comics/purity.png

Now that biologists can generate millions of data points from a single sample, it is often assumed that fundamental insights will follow. If one takes the beginning of the Human Genome Project(1990) as the start of the genomics era, we are now 30 years in and still at the stage of large-scale stamp accumulation. The sheer size of a new data set remains one of the major selling points for new papers, and significant time and resources continue to be devoted to the generation of new biological data. Whereas one might have wished for early quantitative breakthroughs from all of this new data, the most obvious short-term effect of genomic technology has been to turn biologists from artisinal into industrial stamp collectors. The fact that the word “landscape” is a staple of high profile genomics papers reflects the degree to which data generation continues to be a primary focus of genomics research.

So, after describing all these landscapes, what comes next? Will genomics be the Bob Ross of science or can we hope that the descriptions of all these landscapes are building towards some kind of quantitative synthesis? Like Einstein in the patent office, is biology’s next quantitative genius is currently designing recommender systems by day and dreaming about fundamental biological principles in her spare time? While it would be great for a new biological synthesis to emerge unexpectedly, most people think that the breakthrough insights in biology will emerge in a more systematic manner through the application of algorithms to big biological datasets. This is where machine learning (ML) comes in.

It is important to avoid a naive faith that ML will magically extract truth from big data. I encounter this ML-centric magical thinking with depressing regularity in biomedicine, and I can personally attest to the many useless ways that ML can be applied to biological data. Too often, the goals of ML-based biology projects are poorly defined, with ML playing a deus ex machina kind of role. These projects don’t adequately account for biological complexity and the limitations of biological data. It’s much easier to use algorithms to identify cats in pictures than to identify the molecular drivers of colon cancer, never mind more detailed questions like why the incidence of early colon cancer is increasing in high income countries. As expert ML practitioners know, domain knowledge is usually an essential ingredient for successful projects.

A compelling roadmap for ML in biology can be found in Yu and Ideker’s “Visible Machine Learning,” which makes use of the Visible V8, a toy engine, as its organizing principle. Just as mechanics need to understand how an engine works in order to repair it, so biologists need to understand how organisms work in order to understand biology and cure diseases. The Visible V8 approximates a true engine closely enough that important lessons about real engines can be learned by studying it. Thus the authors propose that when ML is applied to biological data, the emphasis should be on developing visible (i.e. interpretable) ML models, because the biological insights will come primarily from the structure of the models themselves rather than the model outputs.

Yu et al., Cell 2018

This is a great way of thinking about how to use ML with biological data. In this paradigm, biology in its fully-realized quantitative form will be more like engineering than physics. Like engineers, most biologists are interested in learning about how a specific system works. For example, since my research focus is human lung disease, I am relatively (but not entirely) uninterested in understanding lung disease in hamsters or horses. Biologists study contingent systems with specific evolutionary histories, and therefore biology truths are more context-dependent than physics truths. Much of biological research is motivated by understanding how specific organisms solve specific problems within the constraints of physical laws. In biology, context almost always matters, a fact that informs the main arguments of Yu et al. in favor of visible machine learning in biology.

Data Heterogeneity

Yu et al. point to data heterogeneity as a major challenge for applying ML algorithms to biological datasets. In their words, “biological systems are almost certainly more complex than those addressed by machine learning in other areas.” Imagine that you are given a dataset with one million pictures of cats. A standard ML problem might be to identify the cat in each of the pictures. In contrast, a standard biology ML problem would be more akin to getting one thousand fuzzy pictures with noisy labels, and the task is to find out what kind of animals might be in the pictures.

To get more concrete, a fairly well-formulated ML problem is to take a series of gene expression datasets and infer the gene regulatory model that generated these data. Gene expression is partly governed by other genes, and the regulatory connections between genes can be expressed as a network or graph. The problem can then be formulated as one of learning which graph, from the space of all possible graphs, represents the true gene regulatory model that produced the training data. Data heterogeneity complicates this problem in two ways:

  • the true model may contain redundancies such that identical output can arise from different inputs
  • the data may arise from more than one model, or may be informative for only certain aspects one overall model

With respect to real gene regulatory networks, we know that these networks work differently in different cell types. Some genes, like RFX1, can activate gene expression in one state while inhibiting gene expression under different conditions. The information content of any given biological dataset is often low with respect to the complexity of the generative model, thus, even the biggest biological datasets aren’t really that big relative to the scope of the problem. This is one reason why, 30 years into the genomics era, we are still mapping biological landscapes, and we haven’t yet begun to exhaust the space of possible biological states in need of characterization.

Visible, Interpretable Biological Models

So what do Yu et al. mean by “visible” biological models? They don’t give a precise definition, but they state that visual models incorporate “prior knowledge of biological structure.” Interestingly, this presupposes that biological knowledge is encoded and accessible to algorithms, which is its own challenge. But if one assumes that appropriate encodings are available, visible models are a tool for synthesizing prior biological knowledge and novel data. The defining feature of visible models is that their “internal states” can be accessed for further study. Here, visible essentially means interpretable, and the authors make the strong claim that interpretable biological models reflect causal processes in biological systems.

But how can we know that an interpretable model faithfully recapitulates causal processes? One big problem with the Visible V8 analogy is that we already know that the model is a faithful representation of the real thing, but with biological models there often isn’t a frame of reference based on highly reliable ground truth. Our prior biological knowledge is not extensive enough to be at all comparable to the Visible V8. Yu et al. propose that algorithms should include prior information on biological structures, but this does not really ensure that the “internal states” of these models recapitulate the underlying biological reality at a meaningful level of detail. In fact, as I’m sure the authors would agree, they surely don’t. There is a chicken and egg problem here – if we really knew the biological models we wouldn’t need to do ML, but the model is so complex that we are hoping that ML + data can help us to discover it. Some might respond that “all models are wrong but some are useful,” but the visible ML argument relies upon interpretation of internal model states as if they were causal factors, so it is of course important that the states have some meaningful connection to the true model, i.e. real biological mechanisms.

Rashomon sets

An important problem for the Visible Models framework is that accurate models don’t necessarily have internal states that reflect causal processes. In an excellent opinion piece on interpretable models, Cynthia Rudin points out that equivalent predictive accuracy for the same task is often achieved by several different methods, implying that there is not a single “best” model but rather a set of different but functionally equivalent models. This set of equivalent models is a Rashomon set (a reference to a famous Japanese movie about multiple perspectives on the same event), and Rudin argues that when the Rashomon set is large there is a reasonable chance that it includes an interpretable (but not necessarily causal) model.

Interestingly, Rudin briefly entertains the causal argument – “Why is it that accurate interpretable models could possibly exist in so many different domains? Is it really possible that many aspects of nature have simple truths that are waiting to be discovered by ML?” – but then she opts for a more conservative argument for interpretable models based on Rashomon sets. The fact that the argument for visible models in biology depends on the claim that these models are approximately accurate reflections of nature is problematic. I personally think it is reasonable, but the onus is on the biology ML community to demonstrate that it is possible to generate models in which studying their internal states produces meaningful biological insights. While there are multiple examples of using prior biological knowledge to guide ML, some of which we have adopted in COPD genomics, I would say that the effectiveness of this approach has not yet been conclusively demonstrated.

Encoding (and updating) biological knowledge

Current ML models don’t closely approximate biological systems, except in very specialized experimental situations. Humans, the systems that we care most about, are incredibly complex multi-cellular, multi-tissue systems with long life spans such that even the most intensive genomic data collection would only capture a small fraction of our biological states. Large-scale landscape projects like the ENCODE, Roadmap Epigenomics, and FANTOM projects have generated tens of thousands of datasets using hundreds of assays to capture biological states in human and murine cell types, and we still know relatively little about how these landscapes change in specific disease or cell activation states. The bottom line is that, in the short and medium term, we will be in a data poor situation with respect to the complexity of the true biological model. Accordingly, the visible model approach leans heavily on the incorporation of biological knowledge to constrain the model space, presumably ensuring that the resulting models will be representative of “true biology.”

This solution runs the risk of being trivial if, as is often done, results are validated by referencing back to known biology in a circular manner. If we are going to use biological knowledge as a constraint, we should focus on examining the internal model states that are initialized by prior knowledge before and after training to determine how they have changed, and we need ways to determine whether these changes are good or bad. Yu et al. propose experimental validation as a means to verify biological predictions arising from the examination of internal model states, which is reasonable but resource intensive. Another alternative is to demonstrate that biologically constrained models objectively improve prediction accuracy relative to unconstrained models. Before you object and state that unconstrained models will always outperform constrained or interpretable ones, consider Rudin’s warning against precisely this assumption. To quote her directly, “There is a widespread belief that more complex models are more accurate, meaning that a complicated black box is necessary for top predictive performance. However, this is often not true, particularly when the data are structured, with a good representation in terms of naturally meaningful features.” After all, the ideal amount of complexity for a model is the amount required to capture the true model, additional complexity just invites overfitting.

I agree with Rudin, because we have shown this to be true in our own domain. By incorporating information related to gene splicing into a previously published gene expression predictive model for smoking behavior, we significantly improved prediction accuracy in test data.

The best performing models were deep neural nets that included an isoform-mapping-layer (IML) manually encoded to represent known relationships between exons and transcript isoforms. Interestingly, we know that this information is only partially accurate, but it still provides enough information to clearly boost accuracy. With additional modifications, it should be possible to update the IML with strong patterns of correlated expression between exons that indicate as yet unidentified transcript isoforms. In this scenario, ML is part of a virtuous cycle in which prior biological knowledge in coded structures guides ML discovery, and ML discovery updates these structures. These structures then become continuously evolving repositories of biological knowledge. I would argue that it is this cycle and these structures that are the desired endpoint of biology as a data science – not static formulas like E = mc2, but a continuously evolving encyclopedia of algorithms and data structures that represent the cumulative state of our knowledge regarding the operational rules of a specific biological system.

Deep neural net architecture including isoform-mapping-layer

Final thoughts

So, how should we go from describing genomic landscapes to understanding the rules that shape these landscapes? I agree with Yu et al. in their overall endorsement of interpretable algorithms that integrate prior knowledge with new data. At present the methods to interrogate internal states are vague, and further development in that area is needed. As Rudin states, interpretability is domain specific, and while Yu et al. have begun to define what interpretability means in the biological domain, this needs to be defined more precisely so that standardized comparisons between algorithms can be more readily made. Finally, the biggest challenge is to prove that the internal states of ML models mean anything at all. For many biological problems, the size of the Roshomon set is large. The use of prior biological knowledge to constrain ML models is a natural solution to this problem, but this establishes a new problem of encoding a wealth of biological facts into data structures that can interact with new data via algorithms. Biologists should and will continue to characterize biological landscapes, but we also need an expandable canvas of algorithms and data structures that can link these disparate landscapes into interpretable models of biological systems.

petecastaldiLeave a comment

COPD subtypes: Table of Contents

Welcome to the COPD subtypes blog! This is the place to come for our most up-to-date thoughts about our approaches/findings regarding COPD subtypes. As of January 2020 we have five posts, which are summarized below. For those who want to start with a bigger picture summary, post #5 is the best place to start. Otherwise, if you go through them sequentially that more closely follows our published papers and the natural evolution of our groups’ thinking on subtypes.

1: The COPD continuum and the downsides of clustering. Reviews one of our first subtyping papers and discusses the fact that COPD data usually do not have clear clustering structure.

2: Reproducibility: Disease axes > clusters, a 10 cohort validation study. Reviews our collaborative paper that demonstrates 1) problems with clustering reproducibility in independent data and 2) high similarity of PCA axes across those same cohorts.

3: For COPD, think disease axes before clusters. A brief post that illustrates the importance of defining feature spaces (i.e. the variables that are most important for cluster identification) and introduces supervised learning and disease axes as a promising way to do this.

4: A clustering alternative: supervised prediction for disease axis discovery. Makes the case for an alternative path to clusters that goes first through supervised prediction and disease axes, then to outcome-driven subtypes.

5: What are COPD subtypes for? A higher level summary of how disease axes and supervised learning can be a useful approach.

petecastaldiLeave a comment

#5: What are COPD subtypes for?

We often ask what the subtypes of COPD may be, but it’s less common to ask what we intend to do with the subtypes we want to discover. What are COPD subtypes for? Why do we need to discover them? There are usually two things that people want from a COPD subtype:

  • the subtype accurately captures an aspect of COPD biology
  • the subtype is correlated to an important clinical characteristic or outcome of COPD

An ideal subtype would give us both things at the same time, but I don’t think we’re there yet. There is still a gap between clearly “biological” subtypes and the best predictions we can get using supervised models. When we have subtypes that are clearly “biological” that are also essential for accurate prediction of important COPD outcomes, then perhaps we will have attained something like an updated, biologically-driven COPD classification. It’s clear that we should think of the search for COPD subtypes as a long-term project. Since subtypes can mean different things to different people, trying to solve all of our subtyping needs in one step may not be the most productive approach.

To put things a bit more bluntly, there is a kind of machine learning analysis cycle that usually leads to disappointment, and that I think we should try to avoid. It goes like this:

  • Step 1 (This is going to be great) : We have lots of great data, and we’re going to do machine learning!
  • Step 2 (Unbiased machine learning is great) : We’re going to be unbiased, so we’re going to define some variables/outcomes that we want our subtypes to be associated to, and we’re going to hold these out of the machine learning process to validate what we find.
  • Step 3 (Why isn’t this working) : We did machine learning and found stuff, but that stuff isn’t as strongly associated to our validation measures as we hoped.
  • Step 4 (The unacknowledged descent into supervised learning) : Let’s try to modify our set of input variables and tweak our parameters so that our “validation” metrics look better.
  • Step 5 (The results desert) : We’ve done a lot of things, but we haven’t found a great solution, and we don’t have a good rationale for picking which one of our many clustering results should be the main one (as described in detail in this post).
  • Step 6 (Strategic retreat) : These results aren’t what we’ve hoped, but let’s make some ad-hoc justifications and write this up.

Sound familiar? I’ve been there many times, and it can be frustrating. But it’s important to be honest about the challenges of unsupervised clustering in COPD with the intent of finding the best possible way forward. I think it helps to acknowledge the following things.

We’re a long way from the dream of true, biologically correct COPD subtypes. COPD is complex and difficult to study. We don’t fully understand the natural history and causative factors of COPD, and dividing COPD into its biological subtypes implies a level of understanding that doesn’t yet exist. Paradoxically, we won’t really understand COPD biology and natural history without accounting for its subtypes. So, we need to pull ourselves up by our bootstraps so to speak and iterate between subtype definition and biological discovery.

We should use supervised learning methods rather than focusing exclusively on unsupervised clustering. The ability of supervised models to help identify (or construct) important features can really help us in the first stage of data exploration. Too often, unsupervised clustering yields multiple possible solutions with only modest associations to COPD outcomes and weak justification for choosing a single, “optimal” solution. Supervised methods are much better equipped to discriminate between models and reduce data dimensionality in a way that is relevant to COPD-related outcomes, as discussed here. Using “all the data” in an unbiased manner will not, in and of itself, be sufficient.

Integrating prior knowledge into machine learning studies is essential, and this is for two reasons. First, when machine learning methods are applied to biological problems, we care not only about the accuracy but the interpretability of the model. “Interpretability” in this case means comparing the structure of our models to already known biology (think of gene set enrichment analysis as a crude example of this). Second, even though biology is now a data science, we still don’t have the volume of data required to learn all the necessary parameters for most models by “brute force” (see an excellent review here). The best applications of machine learning to biology typically use biological knowledge to guide parameter selection or model structure. For COPD and other chronic diseases, we need to be prepared to assist our algorithms by “hard-coding” biological knowledge into our models (as here, for example).

We need to be more specific about what we mean by subtype. With respect to subtypes, do we think there a single set of subtypes that capture the essential differences between people with COPD? Maybe. But think about it this way – is there a single set of lung cancer subtypes that capture the important differences between subjects with lung cancer? It’s complicated. Pathology matters – there are important differences between adenocarcinoma and small cell cancers. But molecular markers also matter, especially in light of available treatments. EGFR mutation and expression patterns matter, but so does ALK1, RET, and other genes. Do these markers define subtypes because they are more biologically important than other genes, or is this driven primarily by the fact that we have effective treatments targeting these genes? We want our subtypes to be biologically relevant, clinically useful, and we want machine learning to find this all for us in an “unbiased” manner. But if we’re not careful we end up asking machine learning methods to ask questions that really can’t be answered, at least not with the data we have provided. This is a reason for focusing on outcome-specific subtypes (rather than one-size-fits all subtypes) as an interim measure.

Where this will ultimately end for COPD? We are still in the relatively early stages of learning how to best utilize big datasets of images and genomics. While it seems clear that supervised approaches have promise, it is also true unbiased genomics screens have advanced our biological knowledge significantly. From genome-wide association studies, we now know more than 80 genetic loci that contribute to COPD risk. Detailed functional analysis of individual loci has led to novel functional insights that implicate specific genes, regulatory elements, and cell types, as has been shown for genetic influences on TGFB2 expression in lung fibroblasts. These rich datasets have already produced new biological insights. But we are also now in the post-GWAS era where the challenge is not only to discover disease-associated molecules but also to put them in context and better define their utility and applicability. For these second-order projects, of which subtyping is an example, some degree of supervision will probably lead to more fruitful applications of machine learning.

petecastaldi1 Comment

#4: A clustering alternative: supervised prediction for disease axis discovery

COPD clustering papers often justify the importance of their clusters by demonstrating their association to a meaningful clinical outcome, such as the frequency of respiratory exacerbations or rate of disease progression. In previous posts, the point has been made that the COPD “phenotypic space” is usually a continuum and that continuous “disease axes” provide a more accurate and reproducible summarization of this continuum than clusters. This post describes one possible response to the challenge of poor cluster reproducibility by identifying disease axes through supervised learning. At the end, a way back to subtypes is explored.

First, if the goal is to be able to make better predictions of future COPD outcomes, it’s clear that for disease axes generally outperform clusters, often by a substantial margin. In a paper from 2018, Greg Kinney and colleagues at National Jewish Health used factor analysis to identify four main factors of variability in COPDGene data, including measures from chest CT, spirometry, and functional assessments. Focusing on overall mortality, each of the four factors was significantly associated to mortality, and there was synergistic effect of factors related to emphysema and airways disease on mortality risk, as shown below.

The mortality analysis from Kinney’s paper encourages us to think about defining subtype boundaries based on the distribution of outcome risk is relation to disease axes. Unlike clustering, which defines groups based on similarity in the original clustering space, this approach defines a relevant feature space (defined by disease axes) but then establishes group boundaries based on the local probability of a given outcome. As this paper shows, in the space defined by emphysema and airways disease, the relationship to mortality is non-linear. It would be natural to divide subjects into two groups along the boundary where mortality risk begins to increase sharply. One benefit of this outcome-driven approach to defining subtypes is that it can easily be adapted to other relevant outcomes, for example treatment response.

But what about a head-to-head comparison of outcome prediction for subtypes versus disease axes? In a 2019 paper in Thorax, we used prediction models to generate subtype-oriented disease axes (SODAs). Unlike disease axis from factor analysis or PCA, the use of supervised learning to generate SODAs allows the user more explicit control over what their disease axes mean/represent. In factor analysis and PCA, the orientation of a disease axis is determined by the correlation structure of the original data. While this is often desirable, it means that axes are determined by the initial selection of variables. SODAs on the other hand are determined by:

  • the response variable, which in this case is a binary variable encoding two subgroups of subjects (i.e. subtypes)
  • input or predictor variables

To make a SODA, we build a predictive model using the two subtype groups (i.e. subtypes) as a binary response and the input variables as predictors. For example, if you specify a group of “pure airways disease” subjects and another group of “emphysema predominant subjects”, then the resulting SODA axis can be thought of as a line with airways disease at one end and emphysema at the other. Importantly, the SODA model can be built with a subset of subjects and then applied to the entire dataset.

Using that method, you can generate SODAs and compare them directly to their “parent” subtypes. In 4,726 subjects from COPDGene with 5-year followup data we generated 6 SODAs from 6 subtype pairs, and we compared the predictive performance of the SODAs to their corresponding subtypes with respect to five-year prospective change in FEV1 and CT emphysema. As shown in the table below, SODAs consistently explained more variance in COPD progression than subtypes. If you put SODAs and subtypes in the same models (Table 2 from the paper), the SODAs were nearly always significant (9 out of 12 models) whereas the subtypes were not (4 out of 12).

If one focuses only on the subtype of chronic bronchitis (per the ATS-DLD definition), the bronchitis SODA explains nearly twice as much of the 5-year change in emphysema as the original variable. Why is this? First of all, let’s look at how the chronic bronchitis SODA is distributed according to chronic bronchitis status at baseline and at the follow-up visit.

It is evident that the values of the SODA are shifted as one would expect. Subjects with persistent chronic bronchitis (the P-CB group, i.e. chronic bronchitis at baseline and at five-year followup) have higher SODA values than those without chronic bronchitis (the left group) or those with bronchitis at only one visit (the two middle groups). Importantly, the SODA models were built using information only from the baseline visit.

It’s also fun to look at loess curves of the relationship between the bronchitis SODA and prospective five year changes in FEV1 and emphysema. You can see why the emphysema prediction is particularly strong.

So, how is it that a SODA that is trained by a subtype can actually predict better than the subtype itself? The biggest reason is that the SODA models have access to a lot of information beyond the subtype assignment, namely through their access to the predictor variables. The regression model can be thought of as a filter for the predictor variables. It sorts through the predictors, keeping only those aspects of the variability that are relevant to the subtype. In the case of the chronic bronchitis SODA, it includes not just chronic bronchitis information, but other relevant aspects of FEV1, CT emphysema, and airway hyperresponsiveness. It turns out that, in addition to being relevant to chronic bronchitis, this information is also relevant to future emphysema progression.

So perhaps I’ve convinced you that disease axes are great and the way to go, at least in certain cases. But sometimes you just need subgroups, not axes. For these situations, there is a way to get back to subgroups, and that way is probably more principled and reproducible than clustering. To extend our earlier idea about defining subgroups according to the distribution of outcome risk within a relevant feature space, we can do this for the bronchitis SODA using classification trees, for example. The image below shows subgroups defined solely by cutpoints in the bronchitis SODA, where cutpoint locations were determined by maximizing the difference in CT emphysema progression between groups. The box and whisker plots below show the distribution of change in Perc15 values for each of the bronchitis SODA subgroups. (This analysis was done at an earlier time when there were fewer COPDGene subjects with available follow-up data, hence the smaller numbers.)

To sum up, this post describes an alternative to clustering that relies heavily on supervised learning to define disaease axes, but it can bring you back to subgroups if you wish, and those subgroups are more likely to be relevant for a given outcome than unsupervised clusters. If we are concerned primarily about the association of our subtypes to some important COPD measure (and we usually are), then it makes sense to incorporate supervised learning early in the subtype identification process to define relevant feature spaces for subsequent cluster/subtype identification.

petecastaldi3 Comments

#3: For COPD, think disease axes before clusters

Two previous posts illustrate that COPD clinical data usually forms a continuum without clusters with the resulting effect that COPD clustering is often poorly reproducible. So why are there still so many clustering papers? I think this is because we now have much more complex COPD datasets than we used to, and if you wish to use these data to find novel COPD subtypes, clustering is a natural first step. However, the reproducibility challenges cannot be ignored, so there is a need to find alternative applications of machine learning to help is find reproducible and clinically-relevant patterns in our rich datasets.

When defining COPD subtypes, one of the first challenges is to identify the proper feature space in which subtypes should be defined/discovered. For most data sets, we’re usually not interested in all of the variables, but only in some subset that are relevant to what we’re interested in. But picking that subset is more art than science, so it’s worth spending some time to illustrate this fairly obvious but often under-emphasized aspect of clustering. It’s easiest to visualize spaces in three dimensions, so let’s stick with that for COPD and explore two different COPD feature spaces. The first one is defined by FEV1, FEV1/FVC, and CT emphysema. For contrast, let’s view that space side by side with a space defined by emphysema, airway wall thickness, and the number of exacerbations in the previous year. These data are from ~5,000 subjects in the COPDGene Study second study visit.

While the spaces share one variable (% of emphysema on CT), the overall distribution of these data points is quite different, as you can see by the loss of order of the GOLD stages in the figure on the right. Both spaces seem to have a fairly continuous distribution of points within what seems to be a roughly conical or triangular shape, and neither space has distinct clusters. Clustering performed on these two spaces would produce very different results for the same subjects, highlighting the importance of choosing the feature space. While clustering is often touted as unbiased data analysis, that description minimizes the critical role played by the selection of user-defined parameters (such as the selection of variables) in determining the final result. At its worst, this use of the term “unbiased” ends up being an empty buzzword that gestures towards the magical ability of machine learning to yield insights from big data. In reality, useful machine learning analyses often rely heavily on human expertise and intuition. When we just let the data “speak for itself”, it often turns out that either no one can understand what the data are saying or the data tell us something we don’t want to hear.

In the case of COPD clustering, the data nearly always tell us quite clearly that, first and foremost, there aren’t any distinct clusters. We have also shown how the selection of the feature space for clustering is usually a biased choice made by people rather than algorithms. In this case, bias isn’t necessarily bad, it just refers to the fact that an informed person knows things about their data that algorithms do not.

So, rather than naively apply clustering, what should we do? It’s often useful to perform dimension reduction as first step in analyzing a rich data set to identify dominant trends in the data and focus on understanding those (as done here). Dimension reduction preserves the continuous nature of how COPD data are dispersed in relevant feature spaces, and as a result it provides a more accurate summarization of the data. The most commonly used form of dimension reduction is principal component analysis (PCA), which combines variables together in a linear manner (i.e. variables are added together not multiplied) to produce composite variables that can be considered to define key axes of variability. These key axes, or disease axes, are a more accurate way to start making sense of complex data and to define feature spaces for further investigations of COPD heterogeneity.

To sum up, disease axes are more consistent with the underlying continuous nature of COPD data, which is why they are a better first step for analyzing complex COPD data than clustering. Of course, one down side to disease axes is that, with common methods like PCA, users have little control over the precise aspects of variability that end up being captured by PCA. To address that issue, we have shown how how supervised prediction methods can be a tool for identifying disease axes that have a very clear and specific meaning. As a bonus, these disease axes often provide more accurate prediction of future COPD events than subtype do.

petecastaldi1 Comment